procedural
Categories: re
2021-02-09
by not_really
procedural
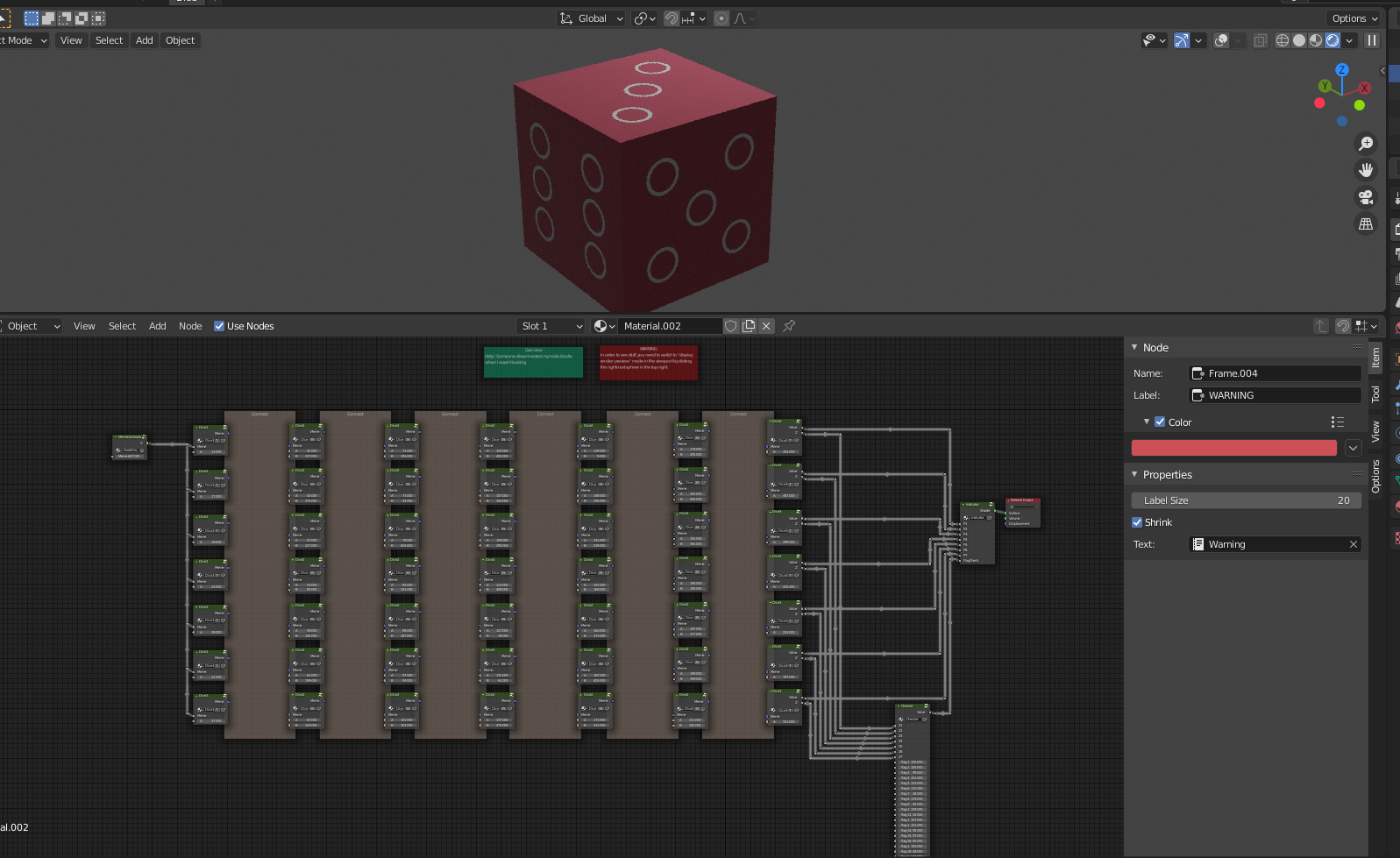
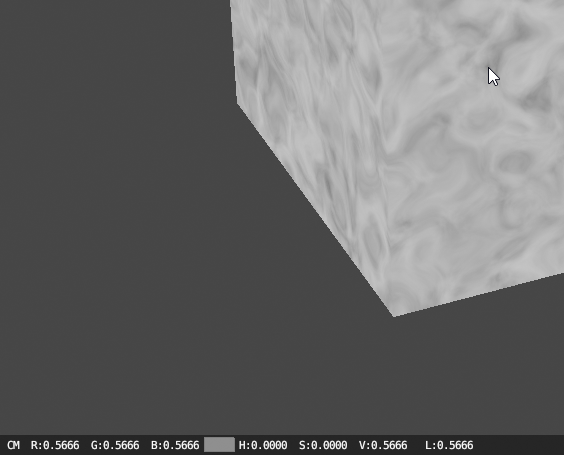
A blender scene with some crazy shader graph.
A message at the top tells us that the node blocks need to be connected, assumingly in a certain correct order.
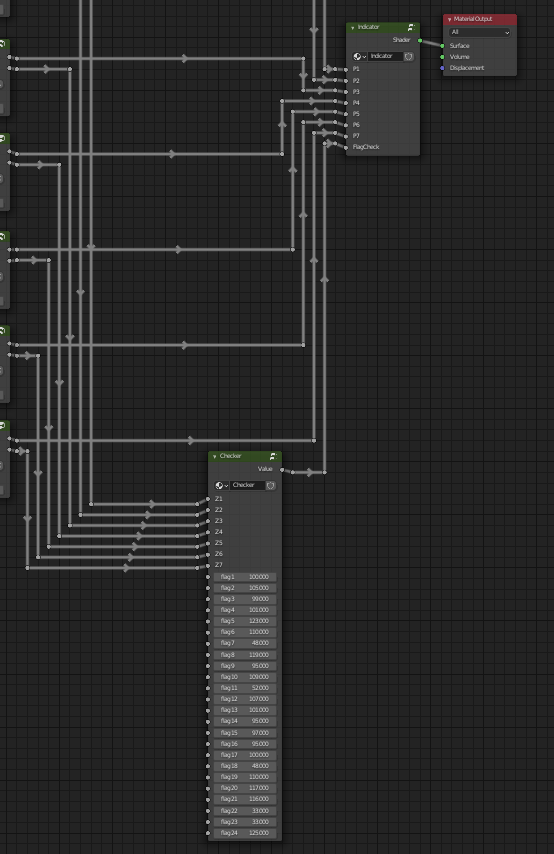
There’s two things that happen after this, the Indicator and the Checker.
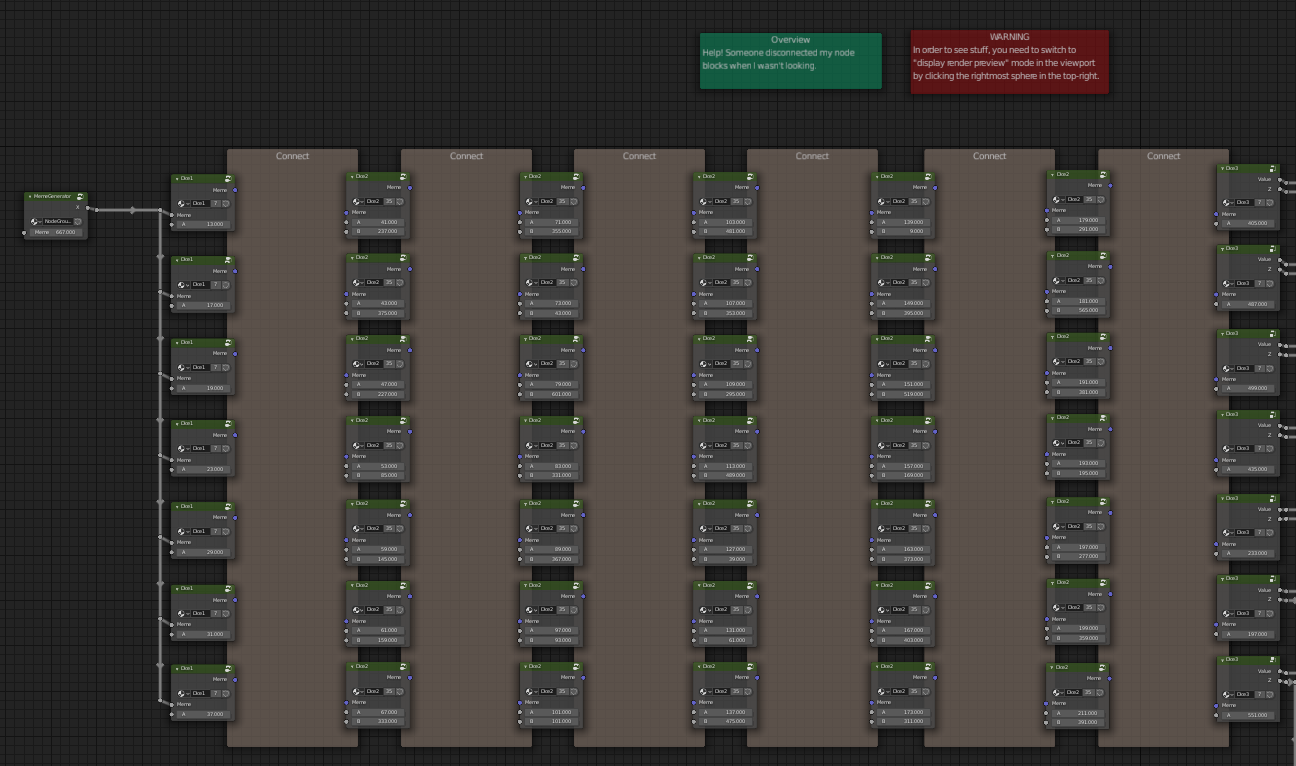
You can break the connections to these node groups by dragging away from the spot it’s connected to. This allows you to type any number you want so you can see what it does.
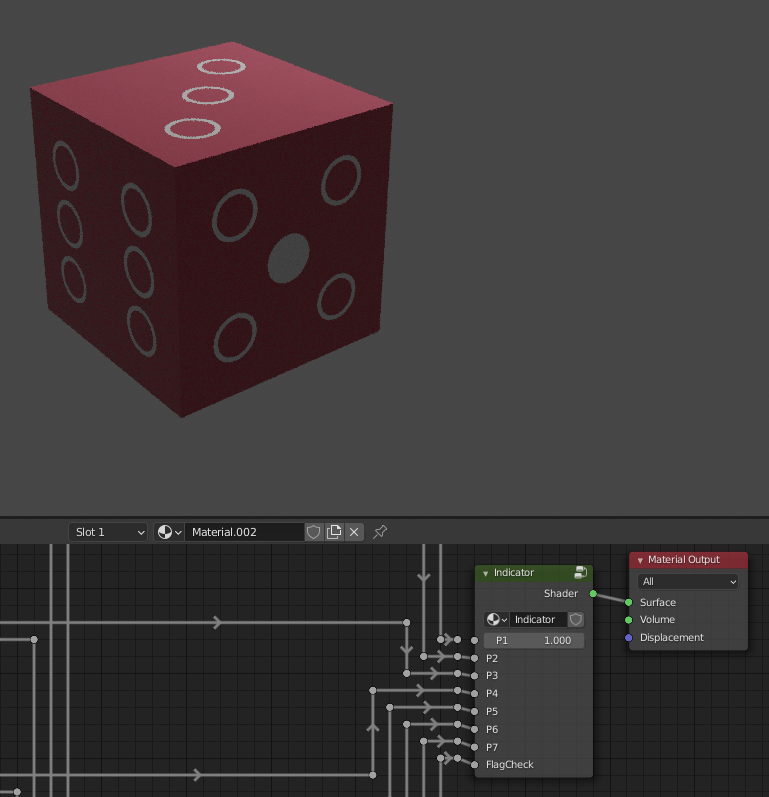
By playing with the values, we find out that in Indicator, P1-P7 control the dots on the cube to be filled and FlagCheck changes the color from red (0) to green (1). We’ll look at the Checker group later, since it looks like something we should figure out after we make the connections.
If you’re not too familiar with shaders, this shader is essentially a function that runs for each pixel on the cube. So in our case, this isn’t a function we run once with one true or false value, this is a function called many times returning different true and false values depending on the pixel.
For example, you can hook up some wires randomly and get a sort of grayed out dot on the cube.

Something that makes this a little harder is MemeGenerator, which doesn’t give us the same starting value for every pixel.
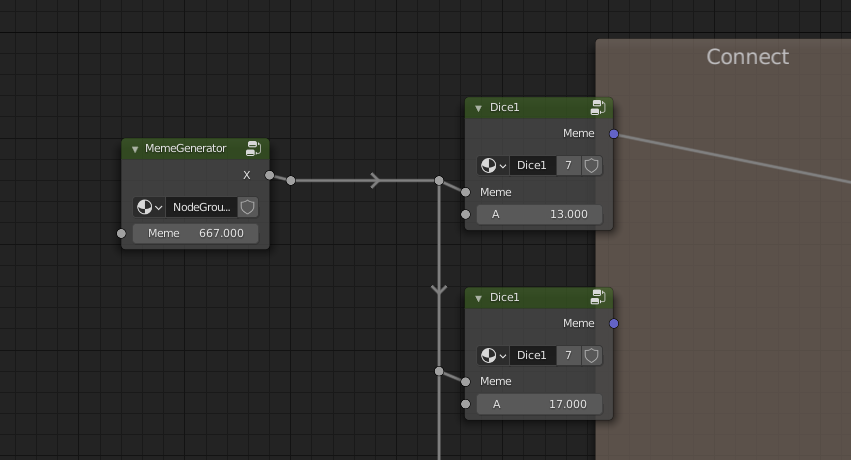
If we connect MemeGenerator directly to output and change the Meme value to something visible like 2, we can sort of get an idea of what’s happening.
If we click the icon on the top right of MemeGenerator we can see what’s going on.
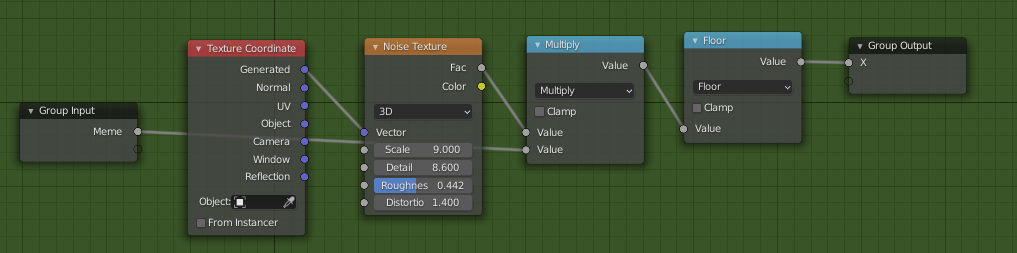
This acts something like this
return floor(pixel_value_in_noise_texture(x, y) * Meme)
By looking at the pixel values in the render, this Noise Texture outputs a value from about 0.5-0.8, so you can get values from about 333-534 from MemeGenerator depending on the pixel. That’s not to say there aren’t pixel values of 600 or even 667. It’s just that a majority of the pixels are of in this range.
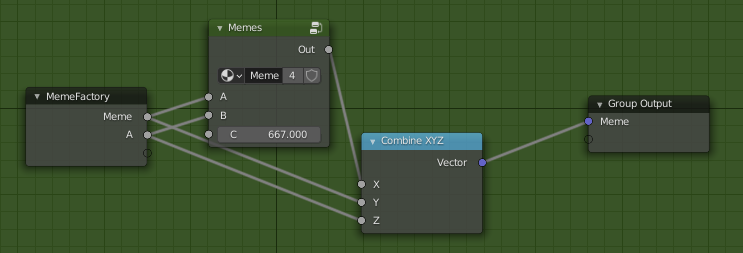
So now that we know what kind of values are coming out of MemeGenerator, it’s time to look at the meat of the “code”, Dice1-Dice3 from the “connect the wire” nodes. They’re pretty much more of the same of each other, so I’ll just show Dice1.
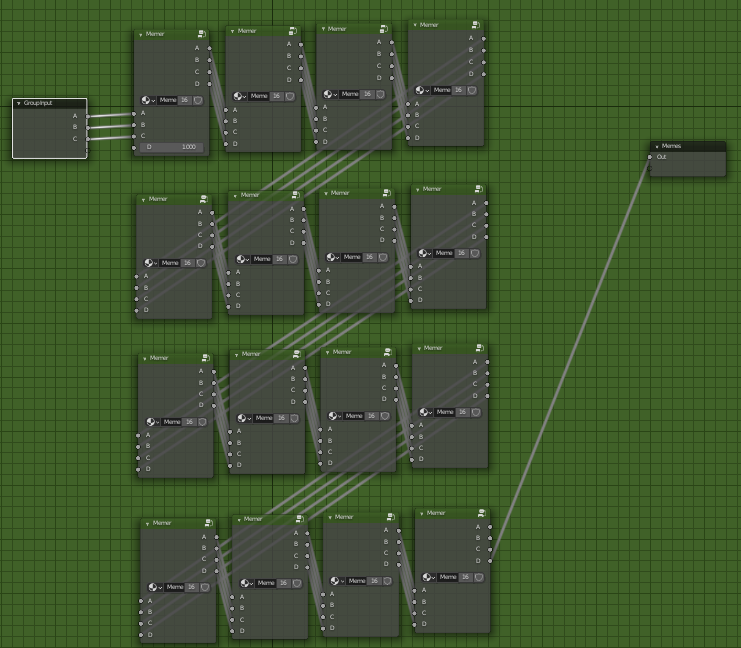
It calls Memes which looks like this.
And Memer looks like this.
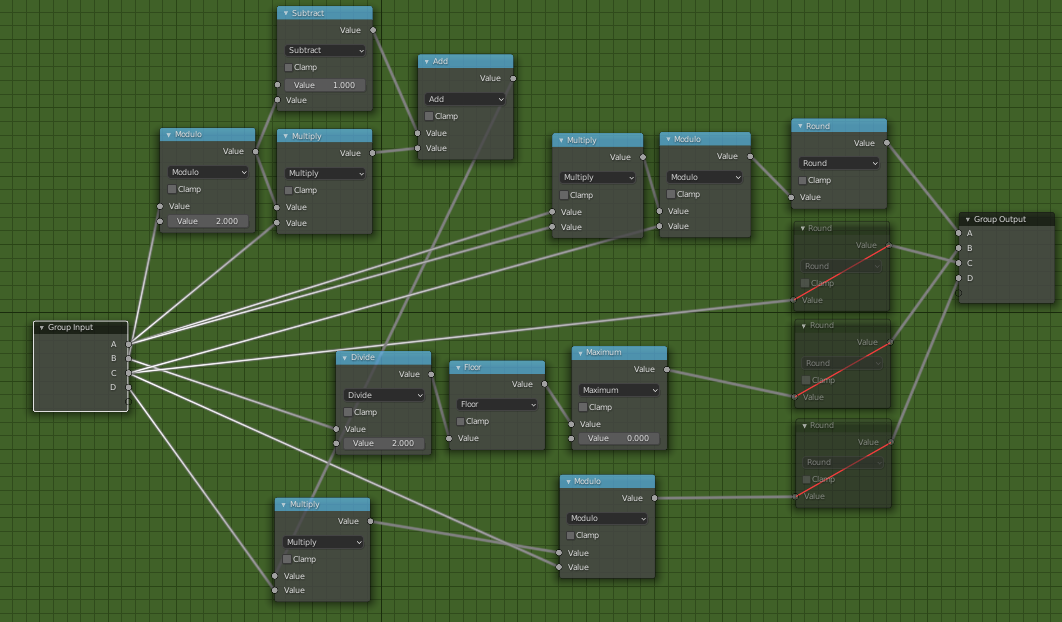
It takes a bit of time to figure out what all these nodes are doing, but we can make python code that should do roughly the same thing. It’s always easiest for me to start from the end and work my way backwards, so that’s what I did here.
Also, if you’ve ever used something like Unreal’s blueprints, this feels kind of similar.
def roundMute(v): #muted node, so it's basically commented out
#return round(v)
return v
def Memer(A, B, C, D):
outA = round((A*A) % C)
outC = roundMute(C)
outB = roundMute(max(math.floor(B/2), 0))
bmod2 = B%2
outD = roundMute((((1-bmod2)+(bmod2*A))*D)%C)
return (outA, outB, outC, outD)
def Memes(A, B, C):
(mA, mB, mC, mD) = Memer(A, B, C, 1)
(mA, mB, mC, mD) = Memer(mA, mB, mC, mD)
(mA, mB, mC, mD) = Memer(mA, mB, mC, mD)
(mA, mB, mC, mD) = Memer(mA, mB, mC, mD)
(mA, mB, mC, mD) = Memer(mA, mB, mC, mD)
(mA, mB, mC, mD) = Memer(mA, mB, mC, mD)
(mA, mB, mC, mD) = Memer(mA, mB, mC, mD)
(mA, mB, mC, mD) = Memer(mA, mB, mC, mD)
(mA, mB, mC, mD) = Memer(mA, mB, mC, mD)
(mA, mB, mC, mD) = Memer(mA, mB, mC, mD)
(mA, mB, mC, mD) = Memer(mA, mB, mC, mD)
(mA, mB, mC, mD) = Memer(mA, mB, mC, mD)
(mA, mB, mC, mD) = Memer(mA, mB, mC, mD)
(mA, mB, mC, mD) = Memer(mA, mB, mC, mD)
(mA, mB, mC, mD) = Memer(mA, mB, mC, mD)
(mA, mB, mC, mD) = Memer(mA, mB, mC, mD)
return mD
def Dice1(Meme, A):
return [Memes(Meme, A, 667), Meme, A]
And we can do the same for Dice2 and Dice3.
def Dice2(Meme, A, B):
temp = Memes(Meme[0], A, 667)
outX = Memes(temp, B, 667)
outZ = ((Meme[2]*10)+A)%65536
return [outX, Meme[1], outZ]
def Dice3(Meme, A):
temp = Memes(Meme[0], A, 667)
lhsm = 1 if (abs(temp - Meme[1]) <= 0.1) else 0
rhsm = 1 if (Meme[2] > 0) else 0 #shouldn't happen since %65536
return [lhsm*rhsm,Meme[2]]
Something you can also see here is the first return value from Dice3 is either 0 or 1 which is used for filling the dice dots. That makes it easy to say that if this pixel passes, we return 1, otherwise 0. But anything else in these functions, we don’t really have to understand what they’re doing since we’ll just use z3.
Here’s what we want to do:
* Unique connections between all nodes
* Node connections produce Dice3 that outputs its first value as 1
* To prevent dice being "partially filled", we'll pick a high input value
Seems easy right? Here’s the code to do that.
values1 = [13,17,19,23,29,31,37]
values2_A = [41,43,47,53,59,61,67]
values2_B = [237,375,227,85,145,159,333]
values3_A = [71,73,79,83,89,97,101]
values3_B = [355,43,601,331,367,93,101]
values4_A = [103,107,109,113,127,131,137]
values4_B = [481,353,295,489,39,61,475]
values5_A = [139,149,151,157,163,167,173]
values5_B = [9,395,519,169,373,403,311]
values6_A = [179,181,191,193,197,199,211]
values6_B = [291,565,381,195,277,359,391]
values7 = [405,487,499,435,233,197,551]
c1 = [BitVec(f'{i}', 8) for i in range(7*7)]
s = Solver()
# Dice1
for i in range(7):
s.add(c1[7*i]==i)
# Dice2 & Dice3
for j in range(1, 7):
for i in range(7):
s.add(c1[j+7*i] >= 0)
s.add(c1[j+7*i] <= 6)
# Unique columns (connections)
for i in range(7):
s.add(Distinct(c1[i], c1[i+7*1], c1[i+7*2], c1[i+7*3], c1[i+7*4], c1[i+7*5], c1[i+7*6]))
# This would be the result if the output from MemeGenerator was 665
# I just chose this since it was right under 667
inp = 665
print("brute forcing x1-x7... hold on")
# Simple brute force since I'm too dumb to figure this out with z3
for x1c in range(7):
# we check each path (in the array, each row) at a time
cond = False
x1 = Dice1(inp, values1[x1c])
for x2c in range(7):
x2 = Dice2(x1, values2_A[x2c], values2_B[x2c])
for x3c in range(7):
x3 = Dice2(x2, values3_A[x3c], values3_B[x3c])
for x4c in range(7):
x4 = Dice2(x3, values4_A[x4c], values4_B[x4c])
for x5c in range(7):
x5 = Dice2(x4, values5_A[x5c], values5_B[x5c])
for x6c in range(7):
x6 = Dice2(x5, values6_A[x6c], values6_B[x6c])
for x7c in range(7):
x7 = Dice3(x6, values7[x7c])
if x7[0] != 0:
# give z3 this path since Dice3 == 1
cond = (Or(cond,
And(c1[1+x1c*7]==x2c,
c1[2+x1c*7]==x3c,
c1[3+x1c*7]==x4c,
c1[4+x1c*7]==x5c,
c1[5+x1c*7]==x6c,
c1[6+x1c*7]==x7c
)
))
s.add(cond)
print("done.")
print(s.check())
model = s.model()
results = ([int(str(model[c1[i]])) for i in range(len(model))])
print(results[7*0:7*1])
print(results[7*1:7*2])
print(results[7*2:7*3])
print(results[7*3:7*4])
print(results[7*4:7*5])
print(results[7*5:7*6])
print(results[7*6:7*7])
The array to check is laid out where the each row is the path taken from the starting node. That makes it easy for me to say the columns must all be unique and to be able to calculate Dice3’s value by the row.
brute forcing x1-x7... hold on
done.
sat
[0, 3, 3, 4, 4, 2, 6]
[1, 1, 2, 1, 6, 3, 3]
[2, 2, 4, 2, 3, 5, 2]
[3, 0, 6, 5, 1, 6, 1]
[4, 6, 0, 3, 0, 1, 5]
[5, 5, 5, 6, 5, 0, 4]
[6, 4, 1, 0, 2, 4, 0]
Yay, sat is always good to see.
Let’s see how it looks in blender.
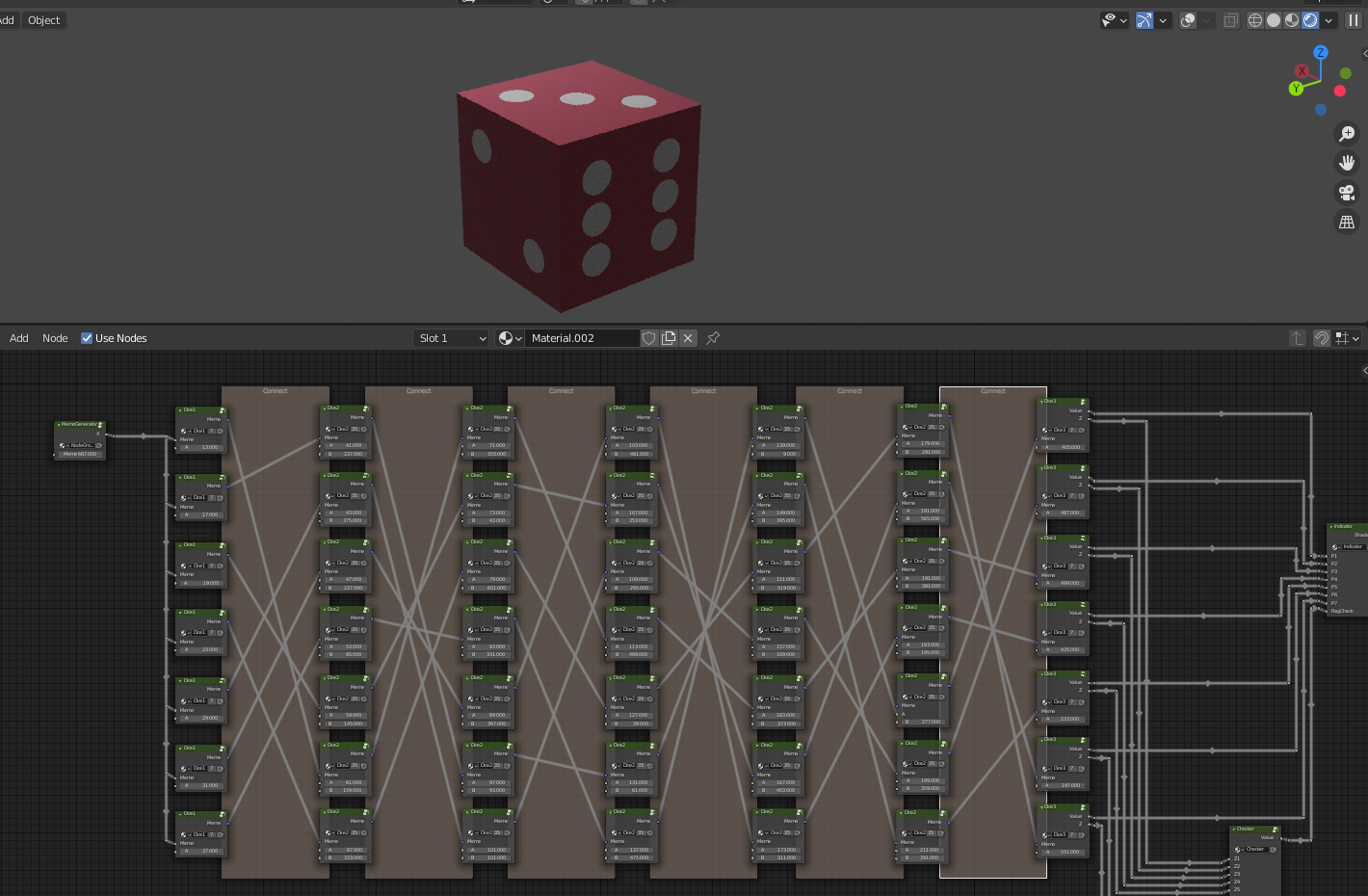
Cube complete! Yay!!!!!
Now all that’s left is the Checker code.
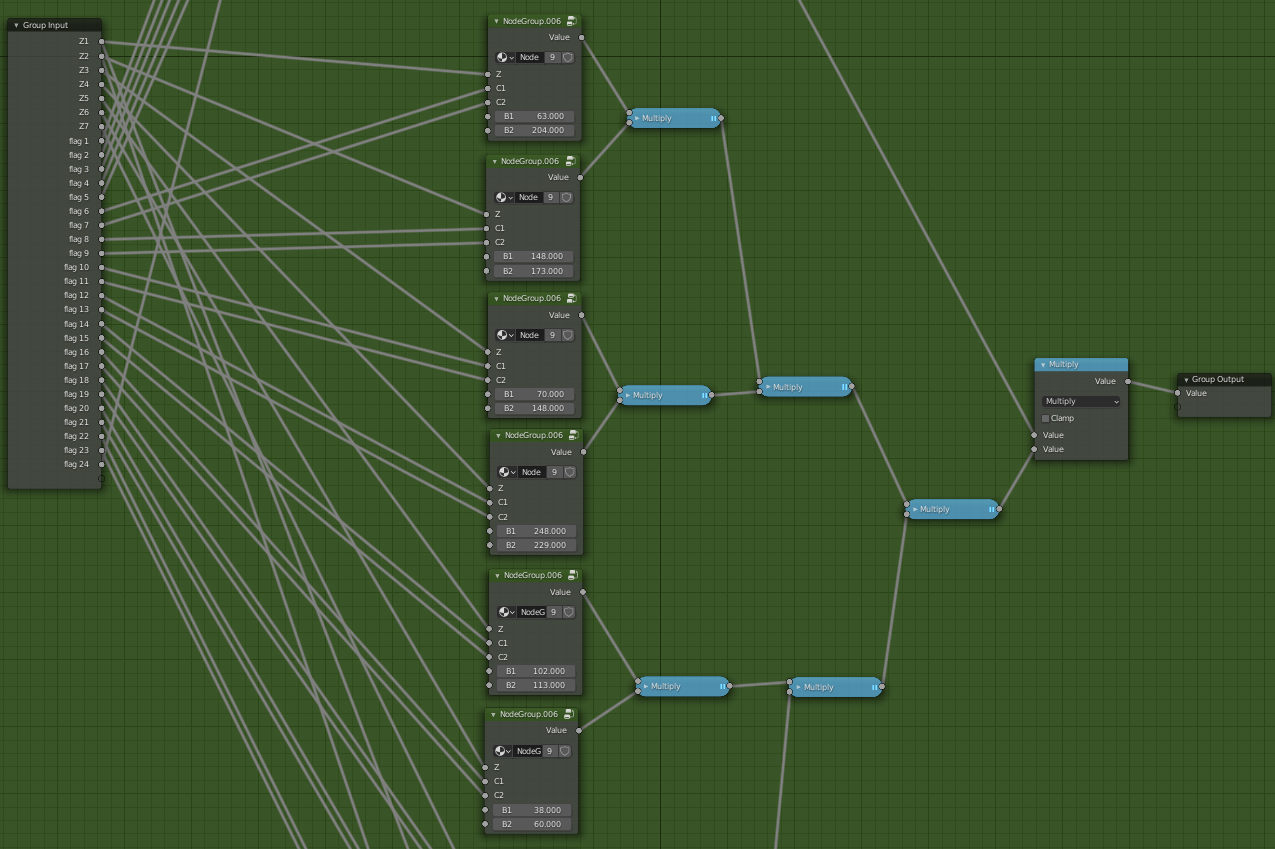
NodeGroup.006 takes five inputs.
* One of the 7 Z values from Dice3 (Z)
* A character in the flag (C1)
* The next character in the flag (C2)
* Some value (B1)
* Some other value (B2)
This seems easy enough, since it looks like only two characters are checked at a time. So it should be easy to brute force, we don’t even need z3 for this.
Here’s the code for Checker and the functions it uses:
def NodeGroup005(Z, Char, Base):
return 1 if (((Z + Char + Base) % 256) <= 0.1) else 0
def NodeGroup006(Z, C1, C2, B1, B2):
return NodeGroup005(Z%256, C1, B1) * NodeGroup005(math.floor(Z/256) % 256, C2, B2)
def Checker(Z1, Z2, Z3, Z4, Z5, Z6, Z7, flag):
# there are checks for dice{} here too but who cares
cond1 = NodeGroup006(Z1, flag[6-1], flag[7-1], 63, 204)
cond2 = NodeGroup006(Z2, flag[8-1], flag[9-1], 148, 173)
cond3 = NodeGroup006(Z3, flag[10-1], flag[11-1], 70, 148)
cond4 = NodeGroup006(Z4, flag[12-1], flag[13-1], 248, 229)
cond5 = NodeGroup006(Z5, flag[14-1], flag[15-1], 102, 113)
cond6 = NodeGroup006(Z6, flag[16-1], flag[17-1], 38, 60)
cond7 = NodeGroup006(Z7, flag[18-1], flag[19-1], 63, 14)
cond8 = NodeGroup006(Z1, flag[20-1], flag[21-1], 56, 136)
cond9 = NodeGroup006(Z2, flag[22-1], flag[23-1], 234, 235)
return (cond1 * cond2 * cond3 * cond4 * cond5 * cond6 * cond7 * cond8 * cond9) == 1
The issue is that we need to get the Z values, but z3 doesn’t give us those, only the path taken. So we’ll have to recalculate Dice1-Dice3 with the right path to get the Z values to plug in.
def GetZValue(x1c, x2c, x3c, x4c, x5c, x6c, x7c):
x1 = Dice1(inp, values1[x1c])
x2 = Dice2(x1, values2_A[x2c], values2_B[x2c])
x3 = Dice2(x2, values3_A[x3c], values3_B[x3c])
x4 = Dice2(x3, values4_A[x4c], values4_B[x4c])
x5 = Dice2(x4, values5_A[x5c], values5_B[x5c])
x6 = Dice2(x5, values6_A[x6c], values6_B[x6c])
x7 = Dice3(x6, values7[x7c])
return x7[1] # Z value
# order by last element (since the first Dice3 is Z1, second Dice3 is Z2, etc...)
Zarr = []
Zarr[results[6+7*0]] = getZValue(*results[7*0:7*1])
Zarr[results[6+7*1]] = getZValue(*results[7*1:7*2])
Zarr[results[6+7*2]] = getZValue(*results[7*2:7*3])
Zarr[results[6+7*3]] = getZValue(*results[7*3:7*4])
Zarr[results[6+7*4]] = getZValue(*results[7*4:7*5])
Zarr[results[6+7*5]] = getZValue(*results[7*5:7*6])
Zarr[results[6+7*6]] = getZValue(*results[7*6:7*7])
Then finally we can brute force each one.
def brute_checker(Z1, Z2, Z3, Z4, Z5, Z6, Z7):
a = [[],[],[],[],[],[],[],[],[]]
for x in range(255):
for y in range(255):
cond1 = NodeGroup006(Z1, x, y, 63, 204) == 1
cond2 = NodeGroup006(Z2, x, y, 148, 173) == 1
cond3 = NodeGroup006(Z3, x, y, 70, 148) == 1
cond4 = NodeGroup006(Z4, x, y, 248, 229) == 1
cond5 = NodeGroup006(Z5, x, y, 102, 113) == 1
cond6 = NodeGroup006(Z6, x, y, 38, 60) == 1
cond7 = NodeGroup006(Z7, x, y, 63, 14) == 1
cond8 = NodeGroup006(Z1, x, y, 56, 136) == 1
cond9 = NodeGroup006(Z2, x, y, 234, 235) == 1
if cond1:
a[0].append(chr(x) + " " + chr(y) + f" {x}, {y}")
if cond2:
a[1].append(chr(x) + " " + chr(y) + f" {x}, {y}")
if cond3:
a[2].append(chr(x) + " " + chr(y) + f" {x}, {y}")
if cond4:
a[3].append(chr(x) + " " + chr(y) + f" {x}, {y}")
if cond5:
a[4].append(chr(x) + " " + chr(y) + f" {x}, {y}")
if cond6:
a[5].append(chr(x) + " " + chr(y) + f" {x}, {y}")
if cond7:
a[6].append(chr(x) + " " + chr(y) + f" {x}, {y}")
if cond8:
a[7].append(chr(x) + " " + chr(y) + f" {x}, {y}")
if cond9:
a[8].append(chr(x) + " " + chr(y) + f" {x}, {y}")
print(a[0])
print(a[1])
print(a[2])
print(a[3])
print(a[4])
print(a[5])
print(a[6])
print(a[7])
print(a[8])
Running it, we get:
brute forcing x1-x7... hold on
done.
sat
[0, 5, 0, 3, 4, 2, 2]
[1, 0, 5, 5, 1, 6, 4]
[2, 4, 1, 1, 5, 1, 5]
[3, 6, 2, 4, 2, 0, 6]
[4, 1, 6, 2, 3, 5, 1]
[5, 2, 4, 0, 6, 3, 3]
[6, 3, 3, 6, 0, 4, 0]
['b ) 98, 41']
['\x97 È 151, 200']
[]
['Q \x17 81, 23']
['± © 177, 169']
['\x1b x 27, 120']
['d 4 100, 52']
['i m 105, 109']
['A \x8a 65, 138']
Oof, that doesn’t look good. One of them didn’t get any solutions, and the rest are mostly unprintable.
My solution was to filter out only printable characters. To do that, we also need to filter possible Z values.
def test006(B1, B2):
options = []
# note that in Dice2, Z is % 65535, and Dice3's Z is just Dice2's
# that means we can limit Z to 65535 here
for Z in range(65535):
if Z % 500 == 0:
print(f"testing {Z}...")
printable = '0123456789abcdefghijklmnopqrstuvwxyz_,.\'?!@$&<>*:-'
for i in printable:
for j in printable:
s = i + j
if NodeGroup006(Z, ord(i), ord(j), B1, B2) == 1:
options.append(Z)
return options
optionslist = [
test006(63, 204),
test006(148, 173),
test006(70, 148),
test006(248, 229),
test006(102, 113),
test006(38, 60),
test006(63, 14),
# the last two also use Z1 and Z2 so we need to filter these twice
test006(56, 136),
test006(234, 235),
[],
[],
[],
[],
[],
]
I would recommend running this in pypy because python is unbelievably slow at making this list.
Once you run that, you get a huge list of possible Z values, way too big to paste here.
Then we can change the first node brute forcer:
for x1c in range(7):
cond = False
x1 = Dice1(inp, values1[x1c])
for x2c in range(7):
x2 = Dice2(x1, values2_A[x2c], values2_B[x2c])
for x3c in range(7):
x3 = Dice2(x2, values3_A[x3c], values3_B[x3c])
for x4c in range(7):
x4 = Dice2(x3, values4_A[x4c], values4_B[x4c])
for x5c in range(7):
x5 = Dice2(x4, values5_A[x5c], values5_B[x5c])
for x6c in range(7):
x6 = Dice2(x5, values6_A[x6c], values6_B[x6c])
for x7c in range(7):
x7 = Dice3(x6, values7[x7c])
valid = False
if x7[0] != 0: # dice3 is not 0 (1)
# if Z value is either 0 or 1, it needs to
# be printable for the last two nodes too
if x7c == 0 or x7c == 1:
if (x7[1] in optionslist[x7c] and
x7[1] in optionslist[x7c+7]):
valid = True
# otherwise, check the list like normal
else:
if x7[1] in optionslist[x7c]:
valid = True
if valid:
cond = (Or(cond,
And(c1[1+x1c*7]==x2c,
c1[2+x1c*7]==x3c,
c1[3+x1c*7]==x4c,
c1[4+x1c*7]==x5c,
c1[5+x1c*7]==x6c,
c1[6+x1c*7]==x7c
)
))
s.add(cond)
brute forcing x1-x7... hold on
done.
sat
[0, 0, 2, 4, 2, 5, 6]
[1, 4, 0, 2, 4, 0, 2]
[2, 2, 4, 1, 5, 6, 3]
[3, 1, 1, 0, 6, 2, 1]
[4, 3, 5, 3, 3, 1, 0]
[5, 5, 6, 5, 1, 4, 5]
[6, 6, 3, 6, 0, 3, 4]
['n 0 110, 48']
['w _ 119, 95']
['m 4 109, 52']
['k e 107, 101']
['_ a 95, 97']
['_ d 95, 100']
['0 n 48, 110']
['u t 117, 116']
['! ! 33, 33']
We got it! We can fill out the Checker with the ascii values of the flag and get a green cube.
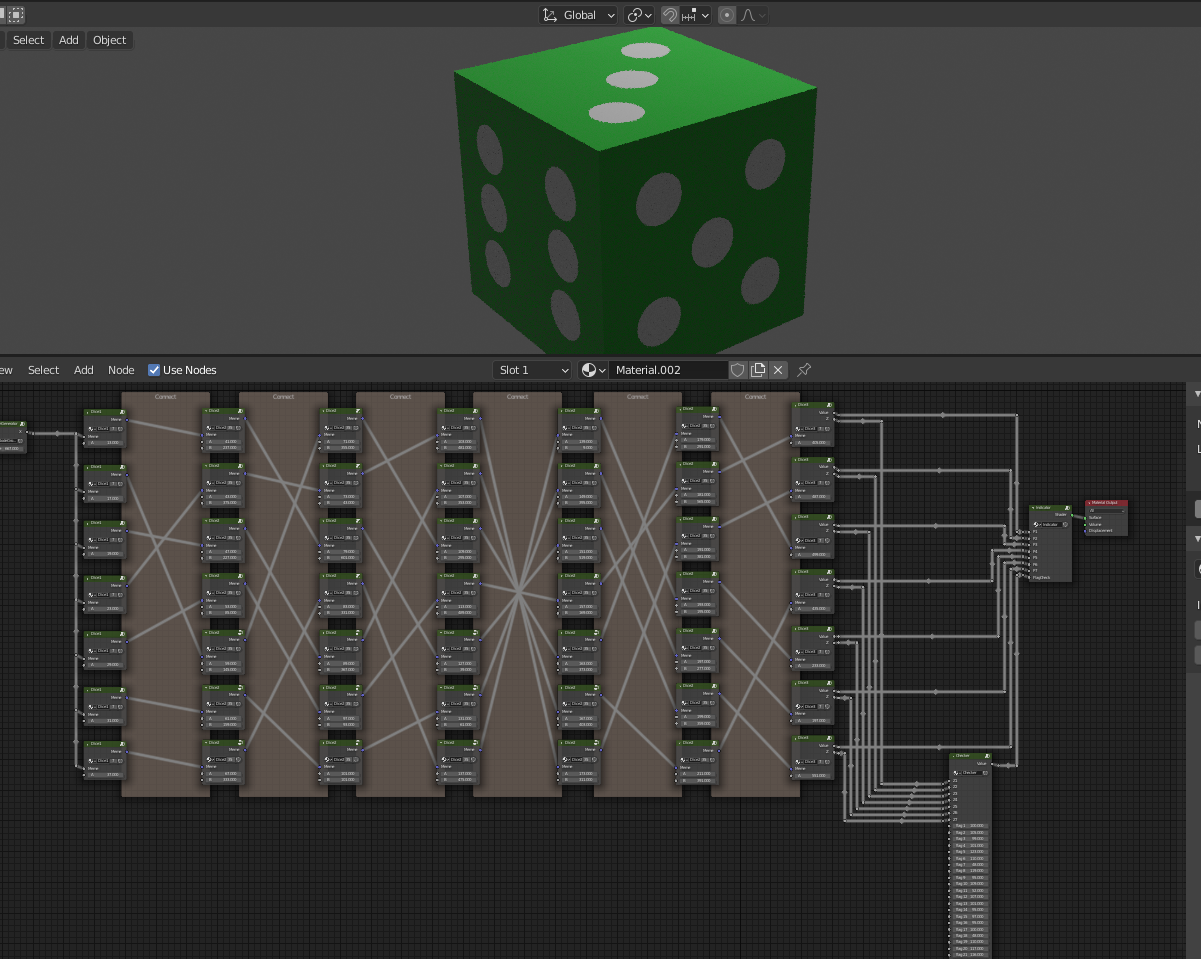
Solve files:
procedural_options.py (narrows down Z results to ascii)