LACTF 2023 - pbr
Categories: re
2023-02-12
by not_really
rev/pbr
pbr is a rust/vulkan challenge that shows Ψβρ in 3D characters, along with some water that looks like it’s straight from the famous water shader on ShaderToy.
Decompiling the code is a disaster. IDA wins this time, but it still misses a few things here and there.
The first thing I did was look directly for the shader since the name of the challenge is pbr and I assumed there were some shader shenanigans happening. I found the function called lactf2023_pbr::PBR_SHADER::load and found the line loading the SPIR-V shader from the executable, which I then extracted.
I already had spirv-dis on my path for whatever reason, so I ran the disassembler on the file. I spent a little bit of time working with the disassembly until I realized that spirv-cross is a way better idea. To extract all four functions, I found the names with spirv-cross shaders.dat --dump-resources (although I probably could’ve found these names in a hex editor), then extracted each one with spirv-cross shaders.dat --entry <stage_name>.
Entry points:
pbr_frag (fragment)
pbr_vert (vertex)
sea_frag (fragment)
sea_vert (vertex)
pbr’s shaders are pretty small and nothing seems suspicious except for the fact that it uses an sbox uniform. Further inspection shows that it’s just used for a weird randomized alpha effect:
float _1137 = uv.y * 16.0;
uint _1144 = (_1137 > 4294967040.0) ? 4294967295u : ((!(_1137 >= 0.0)) ? 0u : uint(_1137));
if (_1144 < 16u)
{
float _1153 = uv.x * 32.0;
_out = vec4(fma(_6204.x, 0.800000011920928955078125, _5860.x),
fma(_6204.y, 0.800000011920928955078125, _5860.y),
fma(_6204.z, 0.800000011920928955078125, _5860.z),
float(
(sbox_3._m0[_1144].y >> int(((_1153 > 4294967040.0) ? 4294967295u : ((!(_1153 >= 0.0)) ? 0u : uint(_1153))) & 31u)) & 255));
break;
}
In the main code, we can see that a real sbox array exists and is passed to the shader at startup. So we know it truly is an sbox and there’s nothing weird going on here. The vert pbr shader doesn’t seem to be interesting either.
All that leaves is the water shader. Like I said before, the water looked eerily similar to the ShaderToy one, so I went over there to compare constants.
ShaderLab:
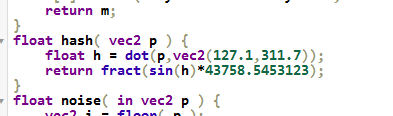
The decompiled water shader:
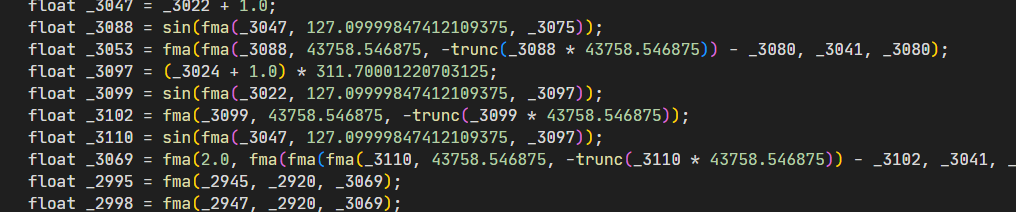
They both have the same very specific constants, so it’s a pretty good chance this is the same shader. (This isn’t a perfect check since other shaders could be using this hash function, but I double checked in many other places and it appears to be the same one, or at least based on it.)
The interesting part is that the code already seems to have separated the real shader from the flag checking code.
And at the very end, 1200 lines later, we get the actual flag checker.
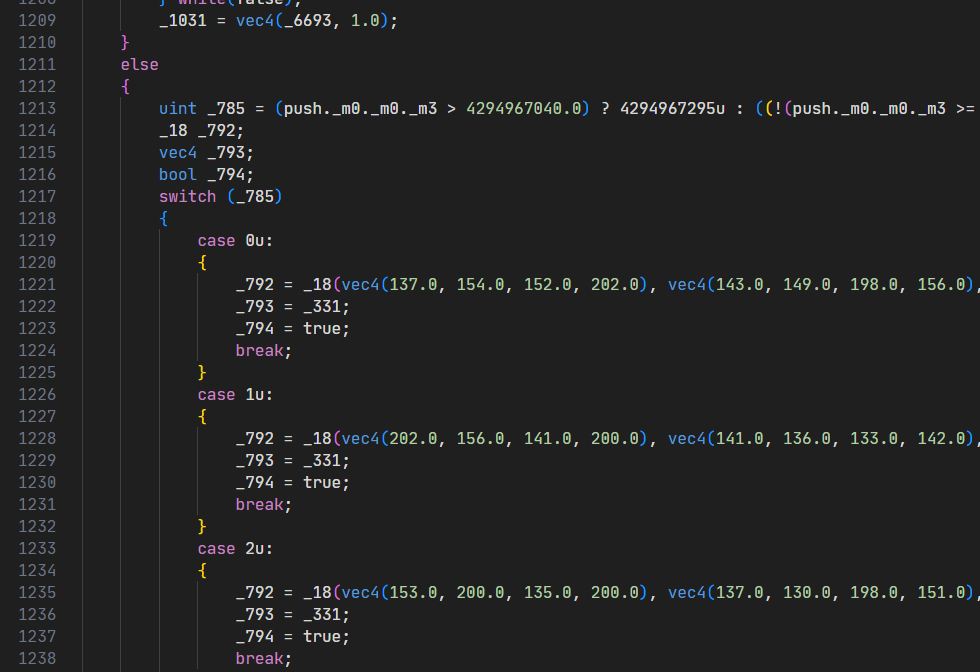
The code is pretty long, so here’s an overview of the different parts.

Part 1
Part 1 takes the value from push._m0._m0._m3 and checks if it’s equal to 0, 1, or 2 and selects a different matrix for each one. If it’s none of them, it picks a zero matrix, but at that point it skips the rest of the code. So we can assume 0, 1, and 2 are the only inputs here.
You might be asking what push._m0._m0._m3 is. The “push” part is referring to push constants, a way to send values to the shader (for all pixels and vertices). It’s a bit easier to look at this in RenderDoc so we can see the values while it’s running. Taking a snapshot and switching to the water shader’s frag program (click one of the blue rectangles on the top of the screen) shows the sbox and push uniforms. This is what the push one looks like.
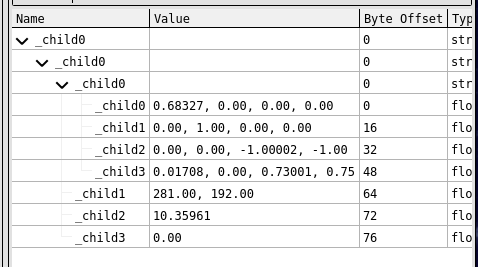
Since we have the code to the original water shader(ish), we can guess that _child1 is the offset and _child2 is the time. _child0 is a matrix (probably not relevant), and _child3 is 0. We’re looking for push._m0._m0._m3, which in RenderDoc would be push._child0._child0._child3. Hmm, that’s not very useful. At this point, I tried spamming my keyboard, clicking all mouse buttons, resizing the window, minimizing the window, etc., but could not get the value to change from anything but 0. Weird, but okay.
Part 2
Part 2 initializes a 69 element array, and loads sbox_1 into it. Looks like we’re loading the sbox again in this shader? But why only the first 69 elements?
Part 3
Part 3’s pseudo code looks like this:
_m3 = _m3_from_part_1
mat = matrix_from_part_1
sbox_list = list_from_part_2
for i in range(69):
if sbox_list[i] == 0:
mat += 1
elif sbox_list[i] == 2:
mat = scramble_mat(mat)
elif sbox_list[i] == 4:
mat = ~mat
idx = (((_m3 + 1) * 70) - 2) - i
if idx < 210:
if sum(mat) != _138[idx]:
fail = True
Where _138 is a list of 210 values, which we’ll see in a bit. The first thing that should jump out to you is that sbox_list is only checked to equal 0, 2, or 4. At first, I thought the switch case I translated this from might be invisibly bit masking the original value or something. But no, it really only seems to be checking 0, 2, or 4. Confused, I went back into RenderDoc to see if I could debug the value of sbox_1. In the pbr shader, the sbox looks as expected, but in the water shader, sbox is empty.
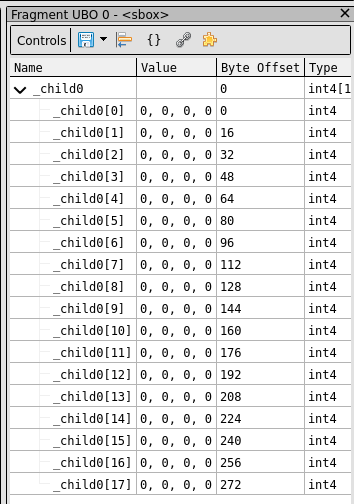
They’ve played us like fools. This is not an sbox. This is a nothing box. Like _m3, I tried my best to fill this array up with anything other than zero through normal keyboard/mouse inputs but failed miserably.
Right, so the sbox may be useless, but what about the _138 array?
const uint _138[210] = uint[](
1583u, 1567u, 2513u, 2497u, 2497u, 2497u, 2481u, 1599u, 1599u, 1599u, 1583u, 2497u, 2497u, 2497u,
2497u, 2497u, 2481u, 2465u, 1615u, 1615u, 1599u, 1599u, 1599u, 1583u, 1583u, 1567u, 2513u, 2513u,
2513u, 1567u, 1567u, 1551u, 2529u, 1551u, 1551u, 1551u, 1551u, 1535u, 2545u, 2545u, 1535u, 1535u,
1535u, 1535u, 1535u, 2545u, 2529u, 2513u, 2497u, 2481u, 2481u, 1599u, 2481u, 2481u, 2465u, 1615u,
1599u, 2481u, 2465u, 2465u, 2465u, 2449u, 2449u, 1631u, 1631u, 2449u, 2433u, 2433u, 1647u, 2433u,
1584u, 1568u, 2512u, 2496u, 2496u, 2496u, 2480u, 1600u, 1600u, 1600u, 1584u, 2496u, 2496u, 2496u,
2496u, 2496u, 2480u, 2464u, 1616u, 1616u, 1600u, 1600u, 1600u, 1584u, 1584u, 1568u, 2512u, 2512u,
2512u, 1568u, 1568u, 1552u, 2528u, 1552u, 1552u, 1552u, 1552u, 1536u, 2544u, 2544u, 1536u, 1536u,
1536u, 1536u, 1536u, 2544u, 2528u, 2512u, 2496u, 2480u, 2480u, 1600u, 2480u, 2480u, 2464u, 1616u,
1600u, 2480u, 2464u, 2464u, 2464u, 2448u, 2448u, 1632u, 1632u, 2448u, 2432u, 2432u, 1648u, 2432u,
1515u, 1499u, 2581u, 2565u, 2565u, 2565u, 2549u, 1531u, 1531u, 1531u, 1515u, 2565u, 2565u, 2565u,
2565u, 2565u, 2549u, 2533u, 1547u, 1547u, 1531u, 1531u, 1531u, 1515u, 1515u, 1499u, 2581u, 2581u,
2581u, 1499u, 1499u, 1483u, 2597u, 1483u, 1483u, 1483u, 1483u, 1467u, 2613u, 2613u, 1467u, 1467u,
1467u, 1467u, 1467u, 2613u, 2597u, 2581u, 2565u, 2549u, 2549u, 1531u, 2549u, 2549u, 2533u, 1547u,
1531u, 2549u, 2533u, 2533u, 2533u, 2517u, 2517u, 1563u, 1563u, 2517u, 2501u, 2501u, 1579u, 2501u
);
I’ve split it up into three groups of 70 based on the code for calculating idx in the pseudo code. Let’s assume that we have _m3 set to 0 and we’re in the first loop. In that case, mat would be this (set in part 1):
mat_m3_0 = [
137, 154, 152, 202,
143, 149, 198, 156,
199, 133, 144, 135,
128, 134, 135, 134
]
And idx would be (((0 + 1) * 70) - 2) - 0 = 68. Weirdly, it checks the index from the very end to the very beginning.
If we sum every number in the matrix together right now, we really do get 2433, the last number in the first block. Looking good so far.
1583u, 1567u, 2513u, 2497u, 2497u, 2497u, 2481u, 1599u, 1599u, 1599u, 1583u, 2497u, 2497u, 2497u,
2497u, 2497u, 2481u, 2465u, 1615u, 1615u, 1599u, 1599u, 1599u, 1583u, 1583u, 1567u, 2513u, 2513u,
2513u, 1567u, 1567u, 1551u, 2529u, 1551u, 1551u, 1551u, 1551u, 1535u, 2545u, 2545u, 1535u, 1535u,
1535u, 1535u, 1535u, 2545u, 2529u, 2513u, 2497u, 2481u, 2481u, 1599u, 2481u, 2481u, 2465u, 1615u,
1599u, 2481u, 2465u, 2465u, 2465u, 2449u, 2449u, 1631u, 1631u, 2449u, 2433u, 2433u, 1647u, 2433u,
^
If we assume sbox[0] == 0 like we saw in RenderDoc, what happens first is that the matrix is incremented by 1 (each number in the matrix is incremented by 1). Starting at index 68 is 1647. However, if we add 16 to the first matrix’s sum, we get 2449, not 1647. So this would not pass.
If sbox[0] was 4 though, it would invert all of the elements in the matrix. This would actually give us a sum of 1647. So it looks like sbox may need to be our input.
I wrote up a quick script for _m3 == 0 to find a string that would be accepted by brute forcing all three options, 0, 2, and 4 for the correct sum. That string ended up being 2002402024224040420024444022220204222004202204242242044222204220422404. Cool, but not useful. How do we get a flag from this?
Part 4
The code for this is short enough, so I’ll paste it here.
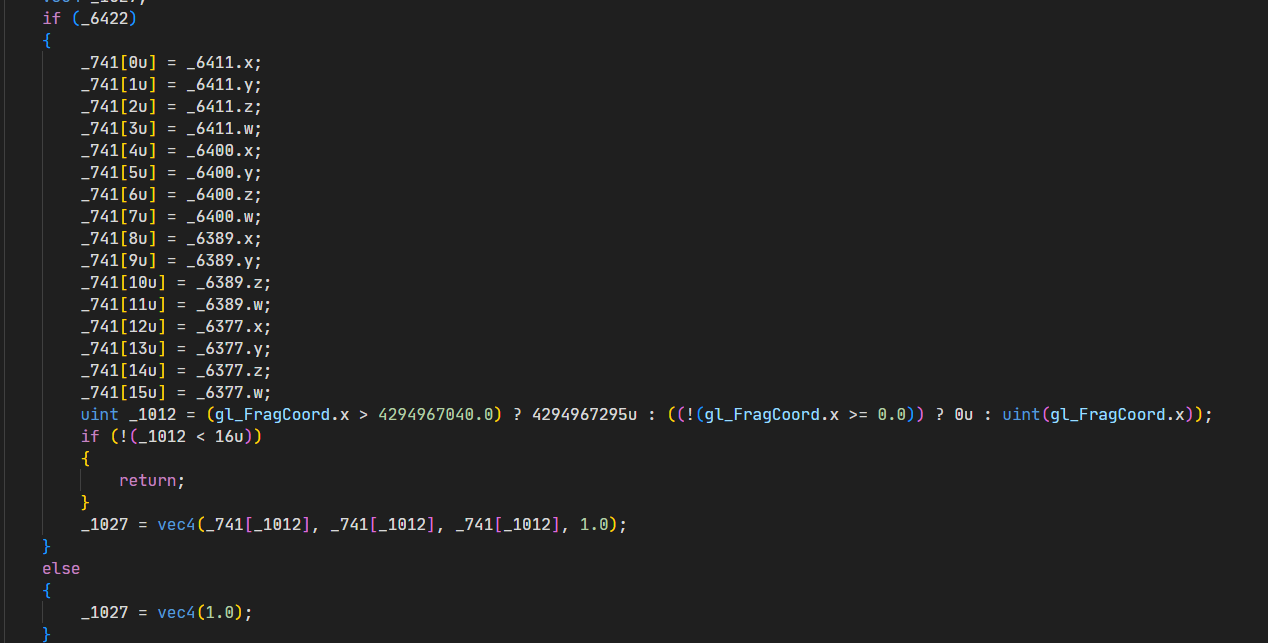
If the x frag coord (x coordinate pixel) is less than 16, set the pixel to a grayscale color of a value in the result matrix (or what I assume is the result matrix). So if the pixel was at x = 5, it would set the value to rgb(mat[1][1],mat[1][1],mat[1][1],1.0).
Is this a grayscale color corresponding to the ASCII value? I printed the end matrix instead of the input in my script. Here was the result:
rac1
lf5_
4vkt
{utu
There’s definitely a flag in there somewhere! It just needs to be unscrambled. I tried multiple things to see if my scramble script was wrong, but it didn’t seem to be. Nothing I changed with the code made it any better, so I decided I was going to do it by hand. The team and I spent a little bit trying to figure it out. We eventually came up with lactf{ru5t_vu1k4n_. There were also two other matrices and lists if _m3 was 1 or 2. After passing those in, I got two more scrambled strings:
1_n3nsvmpa__pr_k
b3t3ry5d}_vt_a3r
Since I was pretty sure this was just a mess up with the scrambled matrices, they should be scrambled at the same indices. And sure enough, they are.
lactf{ru5t_vu1k4n_n_sp1rv_mak3_pr3tty_ba53d_r3v}
Not sure what the input was supposed to be, but this challenge was definitely… challenging.
path_a = [
1583, 1567, 2513, 2497, 2497, 2497, 2481, 1599, 1599, 1599, 1583, 2497, 2497, 2497,
2497, 2497, 2481, 2465, 1615, 1615, 1599, 1599, 1599, 1583, 1583, 1567, 2513, 2513,
2513, 1567, 1567, 1551, 2529, 1551, 1551, 1551, 1551, 1535, 2545, 2545, 1535, 1535,
1535, 1535, 1535, 2545, 2529, 2513, 2497, 2481, 2481, 1599, 2481, 2481, 2465, 1615,
1599, 2481, 2465, 2465, 2465, 2449, 2449, 1631, 1631, 2449, 2433, 2433, 1647, 2433
]
path_b = [
1584, 1568, 2512, 2496, 2496, 2496, 2480, 1600, 1600, 1600, 1584, 2496, 2496, 2496,
2496, 2496, 2480, 2464, 1616, 1616, 1600, 1600, 1600, 1584, 1584, 1568, 2512, 2512,
2512, 1568, 1568, 1552, 2528, 1552, 1552, 1552, 1552, 1536, 2544, 2544, 1536, 1536,
1536, 1536, 1536, 2544, 2528, 2512, 2496, 2480, 2480, 1600, 2480, 2480, 2464, 1616,
1600, 2480, 2464, 2464, 2464, 2448, 2448, 1632, 1632, 2448, 2432, 2432, 1648, 2432
]
path_c = [
1515, 1499, 2581, 2565, 2565, 2565, 2549, 1531, 1531, 1531, 1515, 2565, 2565, 2565,
2565, 2565, 2549, 2533, 1547, 1547, 1531, 1531, 1531, 1515, 1515, 1499, 2581, 2581,
2581, 1499, 1499, 1483, 2597, 1483, 1483, 1483, 1483, 1467, 2613, 2613, 1467, 1467,
1467, 1467, 1467, 2613, 2597, 2581, 2565, 2549, 2549, 1531, 2549, 2549, 2533, 1547,
1531, 2549, 2533, 2533, 2533, 2517, 2517, 1563, 1563, 2517, 2501, 2501, 1579, 2501
]
mat_a = [
137, 154, 152, 202,
143, 149, 198, 156,
199, 133, 144, 135,
128, 134, 135, 134
]
mat_b = [
202, 156, 141, 200,
141, 136, 133, 142,
139, 154, 156, 156,
139, 137, 156, 144
]
mat_c = [
153, 200, 135, 200,
137, 130, 198, 151,
126, 156, 133, 135,
156, 154, 200, 137
]
def add_one(m):
new_m = []
for i in range(16):
new_m.append((m[i] + 1) & 0xff)
return new_m
def scramble(m):
return [
m[10], m[13], m[6], m[12],
m[8], m[7], m[15], m[1],
m[4], m[11], m[9], m[2],
m[5], m[0], m[3], m[14]
]
# by guess
def unscramble(m):
return [
m[4], m[1], m[2], m[11],
m[5], m[12], m[0], m[13],
m[6], m[14], m[7], m[9],
m[15], m[3], m[10], m[8]
]
def invert(m):
new_m = []
for i in range(16):
new_m.append(m[i] ^ 0xff)
return new_m
def solve(m, path):
path = path[::-1]
for step in path:
zero_mat = add_one(m)
two_mat = scramble(m)
four_mat = invert(m)
zero_sum = sum(zero_mat)
two_sum = sum(two_mat)
four_sum = sum(four_mat)
if step == zero_sum:
m = zero_mat
elif step == two_sum:
#m = two_mat
m = m
elif step == four_sum:
m = four_mat
else:
print("something went wrong with the path")
exit(1)
m = unscramble(m)
return "".join(map(chr, m))
final_str = ""
final_str += solve(mat_a, path_a)
final_str += solve(mat_b, path_b)
final_str += solve(mat_c, path_c)
print(final_str)